Lec 5 递归
我们将进入一个新主题:递归。递归在没有一定经验和对其工作原理有一定了解之前可能会感觉有些奇怪和不舒服。因此,我们花费大量时间来实现这个目标:培养对递归的熟练和舒适感,以及更深入的理解。我们将从几个不同的角度来探讨这个问题——除了会看看我们如何在自己的程序中使用递归,也将重点介绍递归在幕后是如何工作的(就我们的环境模型而言),以及我们如何决定是否递归解决方案适用于给定问题(或者是否其他方法可能更好)。如果递归感觉奇怪或不舒服,不用担心;这是一种自然的第一反应,随着时间和实践,这个想法将不再那么可怕,并开始成为我们可以在自己的程序中使用的非常强大的工具。
当函数根据自身定义时,就会发生递归
下面看这个例子,对于非负整数n,有
通常来说,一个递归的定义分为两个部分:
- 1个或多个基本情况(就是不需要通过递归就得到答案)
- 1个或多个递归情况(可减少到基本情况的规则集)
代入一个具体数值,我们有
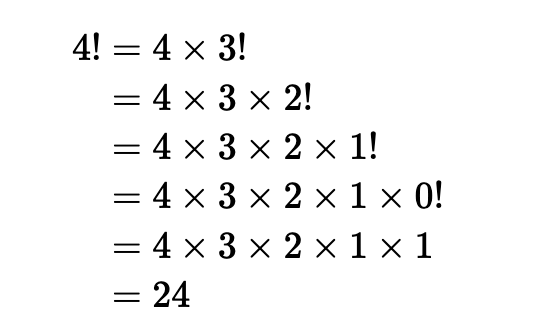
用python实现,
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)在我们继续深入探讨这在 Python 中是如何运作之前,有必要再次提到,根据您先前接触这些概念的程度,编写这样的函数可能会让人感到不舒服。而这里的一个很大的怪异之处在于,当我们编写阶乘函数时,我们在主体中使用了阶乘,尽管我们尚未完成编写阶乘!但是,正确的策略是在假设您有一个完整、可运行的函数版本的前提下编写递归情况,并思考在这些条件下,我如何从递归调用的结果中获取并与其他内容结合以生成我感兴趣的结果?这里我们不需要盲目相信;如果我们设计得当,已经设置了基本情况,并且我们的递归调用朝着这些基本情况的一个递减的方向工作,那么事情将为我们顺利进行。这里另一个奇怪之处在于,在访问对阶乘的某次调用的过程中,我将需要再次调用阶乘,可能会有很多次;而每次调用都有自己的 n 值。所以,我们如何确保 Python 会将这些内容分开并且不会混淆?
递归的环境模型
这表明,递归子问题可以以比数值参数或列表参数的大小或简单性更微妙的方式变得更小或更简单。我们仍然通过将问题从所有可能的整数减少到仅正整数的方式有效地减少了问题。接下来的问题是,假设我们有一个正整数n,比如说n = 829(十进制),我们应该如何将其分解为一个递归子问题呢?想想这个数字,就像我们在纸上写下来的那样,我们可以从8(最左侧或最高位数)或9(最右侧或最低位数)开始。从左边开始似乎很自然,因为那是我们写的方向,但在这种情况下会更困难,因为我们首先需要找到数字的位数以确定如何提取最左边的数字。相反,将n分解为取余b(得到最右边的数字)和除以b(得到子问题,剩下的更高位数数字)的方式更好:
总结
- 每个递归函数都有1个或多个基本情况,1个或多个递归情况
- 递归情况应该让问题变得越来越小或者是越来越简单
