Lec 10 函数式编程

• Lec 10 函数式编程
  • 从迭代到递归
  • Class 到函数
  • 备忘录
  • 装饰器

在编程的早期，有一种叫做LISP的编程语言，是最早能在不同种类计算机上运行的编程语言之一，可以说它在1958年就把函数式编程作为一种实用的编程风格引入了，也是MIT的教职提出的，并且在2007年之前作为必修课程。

本周的实验课将引导你实现你自己的LISP子集。

从迭代到递归

LISP 的一个有趣特性是，它没有任何循环结构（没有 for 或 while 循环）。但它有函数，正如我们之前所见，可以使用函数来实现循环。我们看的第一个例子，阶乘，总是可以这样用循环来写

def factorial(n):
    result = 1
    for i in range(1, n+1):
        result *= i
    return result

尽管 LISP 中没有循环结构，但通过递归函数调用，可以达到与循环相同的效果.

(defun factorial (n)
  (if (<= n 1)
      1
      (* n (factorial (- n 1)))))

或者简化成

def factorial(n):
	return 1 if n <= 1 else n * factorial(n-1)

这个结构使用递归来实现可能看起来有点复杂，但我们将看到我们确实可以做到，使用高阶函数（即接受函数作为输入的函数）。在这里，我们将循环体（即我们希望重复多次的内容）编码为一个函数；然后，我们重复调用该函数，使用递归来跟踪我们还需要运行多少次代码。

下面是一个示例，演示如何使用递归和高阶函数来实现循环：

for i in range(n):
  print('hello', i)
  
# 可以用递归写成
def repeat_n_times(n, func):
    if n == 0:
        return
    func(n)
    repeat_n_times(n-1, func)

Class 到函数

本质上，在Pyhon里面任何类都可以用函数来实现

class Bank:
  def __init__(self):
		self.accounts = {}
  def balance_of(self, account):
    return self.accounts.get(account, 0) # 第二个参数是默认值
  def deposit(self, account, amount):
    self.accounts[account] = self.balance_of(account) + amount
# 使用
>>> b = bank()
>>> b.deposit('Steve', 3)
>>> b.deposit('Mage', 4)
>>> b.deposit('Steve', 5)
>>> b.balance_of('Steve')
8
>>> b.balance_of('Mage')
4

# 函数实现
def bank():
  accounts = {}
  def balance_of(account):
    return accounts.get(account, 0)
  def deposit(account, amount)
  	accounts[account] = balance_of(account) + amount
  return balance_of, deposit
# usage
>>> balance_of, deposit = bank()
>>> deposit('Steve', 3)
>>> deposit('Mage', 4)
>>> deposit('Steve', 5)
>>> balance_of('Steve')
8
>>> balance_of('Mage')
4

重要的是，bank() 返回的两个函数 balance_of 和 deposit 共享一个新创建的封闭帧，其中包含一个新的 accounts 字典。这个帧相当于面向对象版本中的对象。如果细节不清楚，尝试绘制一个环境图。

nonlocal 用法

def counter():
	tally = 0
	def increment():
    tally += 1
    return tally
  return increment

这段代码展示了Python中的一个常见陷阱。即变量 tally 被视为局部变量，而不是从封闭帧继承的变量。为什么会这样呢？

因为当一个函数修改一个变量时，Python强制要求该变量直接存在于该函数的帧中……但在这里，tally 并没有在本地初始化，所以Python会报错 tally 不存在。

但是，Python提供了一种方法来控制这种情况。特别是，如果我们想在 increment 中使用来自封闭帧的变量 tally，我们可以使用 nonlocal 关键字来实现这一点

def counter():
	tally = 0
	def increment():
		nonlocal tally
    tally += 1
    return tally
  return increment

关键字的作用是：它明确指定了 tally 这个变量是在外部封闭函数的帧中定义的，而不是当前 increment 函数的局部变量。

比较一下，bank()为什么就不需要用nonlocal?

Solution: 当一个函数内部要对一个变量进行修改时，默认情况下，Python 会将这个变量视为局部变量。bank 不需要使用 nonlocal accounts 是因为 balance_of 和 deposit 函数并没有重新赋值给 accounts 变量，而是修改字典 accounts 的内容，这种操作不涉及改变变量 accounts 本身的引用，因此不需要 nonlocal。

备忘录

我们可以用更高阶的函数提高性能。

def fib(n):
  if n < 2:
    return n
  return fib(n-2) + fib(n-1)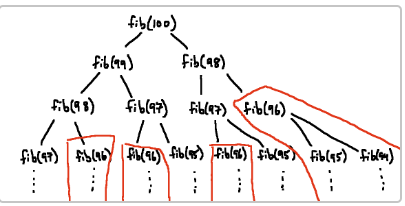

理解上来说，这是在利用**备忘录（memoization）**技术来优化递归算法。斐波那契数列的计算存在大量重复计算的情况，例如 fib(96) 的计算需要 fib(95) 和 fib(94)，而 fib(95) 的计算又需要 fib(94) 和 fib(93)，如此类推，很多中间结果会被反复计算。通过记住已经计算过的结果，我们可以大大减少计算的重复工作，从而提高效率。

# 斐波那契
cache = {}
def fib(n):
	if n not in cache:
    if n < 2:
      cache[n] = n
    else:
      cache[n] = fib(n-2) + fib(n-1)
  return cache[n]

上面代码可以极大提升效率，但它有一个缺点：它使用了一个全局变量。在包含全局变量的大型代码库中，可能会发生各种问题。例如，在同个项目里里面，我用类似方法实现了一个数乘函数如下

# 数乘
cache = {}
def factorial(n):
	if n not in cache:
    if n < 2:
      cache[n] = 1
    else:
      cache[n] = n * factorial(n-1)
  return cache[n]

两函数共享同一个 cache 变量，这将导致混乱！（初始赋值覆盖了现有的全局变量，而不是创建一个新的变量。）我们不希望迫使这两个函数的作者在变量名选择上进行协调。下面将cache放到封闭帧的做法

def fib(n):
	cache = {}
  def __actual_fib(n):
    if n not in cache:
      if n < 2:
        cache[n] = n
      else:
        cache[n] = _actual_fib(n-2) + __actual_fib(n-1)
      return cache[n]
  return _actual_fib(n)

好的，主要的问题已经解决了。不过，你可能也注意到了记忆化斐波那契和阶乘函数之间存在很强的相似性。我们是否可以将这些共同部分提取出来，作为一种可重复使用的组件呢？

装饰器

为了实现这一点， 有一种方法是使用一个类，代码如下：

class MemorizedFunction:
  def __init__(self, func):
    self.func = func
    self.cache = {}
  def __call__(self, *args):
    if args not in self.cache:
      self.cache[args] = self.func(*args)
    return self.cache[args]

这里已经用到了大部分我们之前见过的方法，不过有一个新的技巧是 call 方法。当代码试图像调用函数一样调用某个类实例时，Python 会调用该实例的 call 方法。换句话说，我们可以通过定义如何调用它们来创建自己的新函数。

另一个新的技巧是应用于形式参数的 * 语法，这里称为 *args。这允许函数使用任意数量的实际参数进行调用，这些参数被捆绑在一起形成一个元组，并绑定到形式参数 args 上。（请注意，args 这个名称并没有什么特殊之处。它只是约定俗成地用于处理这种可变长度参数，就像 self 被约定俗成地用于 self 参数一样。而且在 call 魔术方法中使用它并没有什么特殊之处。你可以在你定义的任何函数中使用 * 来处理可变长度参数。）

最后，代码在其主体中还使用了 *args，但我们之前已经见过了——它是解包运算符，所以它将元组解包回函数 func() 的单独参数中。

def fib(n):
  if n < 2:
    return n
  return fib(n-2) + fib(n-1)
fib = MemorizedFunction(fib)

# 如同前面所说，我们并不一定需要类来实现备忘录，函数也可以
def memorize(func):
  cache = {}
  def _mfunc(*args): # 会把他当作元组
    if args not in cache:
      cache[args] = func(*args)
    return cahce[args]
  return _mfunc

# Usage
fib = memorize(fib)

这种使用库函数来增强函数定义的模式非常常见，以至于 Python 为此设计了特殊的语法。我们通过在另一个函数定义之前加上一个 "@" 符号和一个函数名，来表示所谓的装饰器

# 或者使用装饰器形式
@memorize
def fib(n):
	if n < 2:
    return n
  return fib(n-1) + fib(n-1)